Materi matematika volume bangun ruang membahas cara menghitung isi suatu bangun ruang dalam tiga dimensi. Topik ini akan menjelaskan berbagai jenis bangun ruang, rumus volumenya, dan contoh penerapannya dalam kehidupan sehari-hari. Dari kubus hingga bola, kita akan menjelajahi dunia volume bangun ruang dengan mudah dan terstruktur.
Materi ini akan dimulai dengan definisi dan ruang lingkup pembahasan, dilanjutkan dengan rumus volume untuk berbagai bangun ruang seperti kubus, balok, prisma, limas, tabung, kerucut, dan bola. Konsep dasar volume, faktor-faktor yang mempengaruhinya, dan contoh soal akan dibahas secara komprehensif. Selain itu, akan disajikan contoh penerapan dalam kehidupan nyata, dilengkapi dengan soal latihan untuk menguji pemahaman.
Definisi Materi Volume Bangun Ruang
Materi matematika volume bangun ruang mempelajari cara menghitung isi suatu bangun ruang tiga dimensi. Pembahasan meliputi berbagai jenis bangun ruang, mulai dari yang sederhana hingga yang lebih kompleks, dengan rumus-rumus yang spesifik untuk setiap jenisnya. Pemahaman tentang volume bangun ruang sangat penting dalam berbagai aplikasi, seperti perhitungan kebutuhan material konstruksi, kapasitas wadah, dan lain-lain.
Ruang Lingkup Pembahasan
Materi ini akan membahas berbagai jenis bangun ruang, termasuk cara menghitung volumenya. Pemahaman tentang rumus-rumus dasar volume bangun ruang akan dijelaskan secara detail, disertai contoh soal sederhana. Tujuannya adalah untuk memberikan pemahaman yang komprehensif tentang konsep volume pada berbagai bangun ruang.
Jenis-Jenis Bangun Ruang
| Nama Bangun Ruang | Ilustrasi | Rumus Volume | Contoh Soal Sederhana |
|---|---|---|---|
| Kubus | Bangun ruang enam sisi berbentuk persegi yang sama dan kongruen. Semua rusuknya sama panjang. | V = s3, di mana s adalah panjang sisi kubus | Jika panjang sisi kubus adalah 5 cm, maka volumenya adalah V = 53 = 125 cm3 |
| Balok | Bangun ruang dengan enam sisi berbentuk persegi panjang. | V = panjang × lebar × tinggi | Jika panjang balok 4 cm, lebar 3 cm, dan tinggi 2 cm, maka volumenya adalah V = 4 cm × 3 cm × 2 cm = 24 cm3 |
| Prisma Segitiga | Bangun ruang dengan dua sisi alas dan tutup berbentuk segitiga sama dan sejajar, dan sisi-sisi tegaknya berbentuk persegi panjang. | V = Luas Alas × Tinggi | Jika luas alas segitiga adalah 12 cm2 dan tinggi prisma adalah 5 cm, maka volumenya adalah V = 12 cm2 × 5 cm = 60 cm3 |
| Limas Segitiga | Bangun ruang dengan alas berbentuk segitiga dan sisi tegaknya berbentuk segitiga. | V = (1/3) × Luas Alas × Tinggi | Jika luas alas segitiga adalah 15 cm2 dan tinggi limas adalah 6 cm, maka volumenya adalah V = (1/3) × 15 cm2 × 6 cm = 30 cm3 |
| Tabung | Bangun ruang dengan alas dan tutup berbentuk lingkaran yang sama dan sejajar, dan sisi tegaknya berbentuk persegi panjang. | V = π × r2 × t, di mana r adalah jari-jari alas dan t adalah tinggi tabung | Jika jari-jari alas tabung adalah 2 cm dan tinggi tabung adalah 7 cm, maka volumenya adalah V = π × (2 cm)2 × 7 cm = 28π cm3 (atau sekitar 87,96 cm3) |
| Bola | Bangun ruang yang seluruh titiknya berjarak sama dari satu titik pusat. | V = (4/3) × π × r3, di mana r adalah jari-jari bola | Jika jari-jari bola adalah 3 cm, maka volumenya adalah V = (4/3) × π × (3 cm)3 = 36π cm3 (atau sekitar 113,04 cm3) |
Rumus Volume Bangun Ruang
Memahami rumus volume bangun ruang sangat penting dalam matematika. Kemampuan menghitung volume bangun ruang dapat diterapkan dalam berbagai bidang, seperti arsitektur, teknik sipil, dan perencanaan kota.
Kubus
Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam sisi berbentuk persegi yang kongruen. Untuk menghitung volume kubus, kita menggunakan rumus berikut:
Volume Kubus = sisi3
Contoh: Sebuah kubus memiliki panjang sisi 5 cm. Berapakah volumenya? Volume kubus = 5 3 = 125 cm 3.
Balok
Balok adalah bangun ruang tiga dimensi yang dibatasi oleh enam sisi berbentuk persegi panjang. Untuk menghitung volume balok, kita menggunakan rumus:
Volume Balok = panjang × lebar × tinggi
Contoh: Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 4 cm. Berapakah volumenya? Volume balok = 10 cm × 5 cm × 4 cm = 200 cm 3.
Prisma
Prisma adalah bangun ruang tiga dimensi yang memiliki dua sisi sejajar dan kongruen yang disebut bidang alas dan bidang atas, serta sisi-sisi tegak yang berbentuk segi empat. Rumus volume prisma:
Volume Prisma = Luas Alas × Tinggi
Contoh: Sebuah prisma segitiga memiliki luas alas 20 cm 2 dan tinggi 10 cm. Berapakah volumenya? Volume prisma = 20 cm 2 × 10 cm = 200 cm 3.
Limas
Limas adalah bangun ruang tiga dimensi yang memiliki satu sisi berbentuk poligon sebagai alas dan sisi-sisi tegak yang berbentuk segitiga yang bertemu pada satu titik puncak. Rumus volume limas:
Volume Limas = ⅓ × Luas Alas × Tinggi
Contoh: Sebuah limas segiempat memiliki luas alas 30 cm 2 dan tinggi 9 cm. Berapakah volumenya? Volume limas = ⅓ × 30 cm 2 × 9 cm = 90 cm 3.
Tabung
Tabung adalah bangun ruang tiga dimensi yang dibatasi oleh dua lingkaran sejajar dan kongruen sebagai alas dan tutup, serta selimut yang menghubungkan kedua lingkaran tersebut. Rumus volume tabung:
Volume Tabung = π × jari-jari2 × tinggi
Contoh: Sebuah tabung memiliki jari-jari 3 cm dan tinggi 10 cm. Berapakah volumenya? Volume tabung = π × 3 2 cm 2 × 10 cm ≈ 282,74 cm 3 (menggunakan π ≈ 3,14).
Kerucut
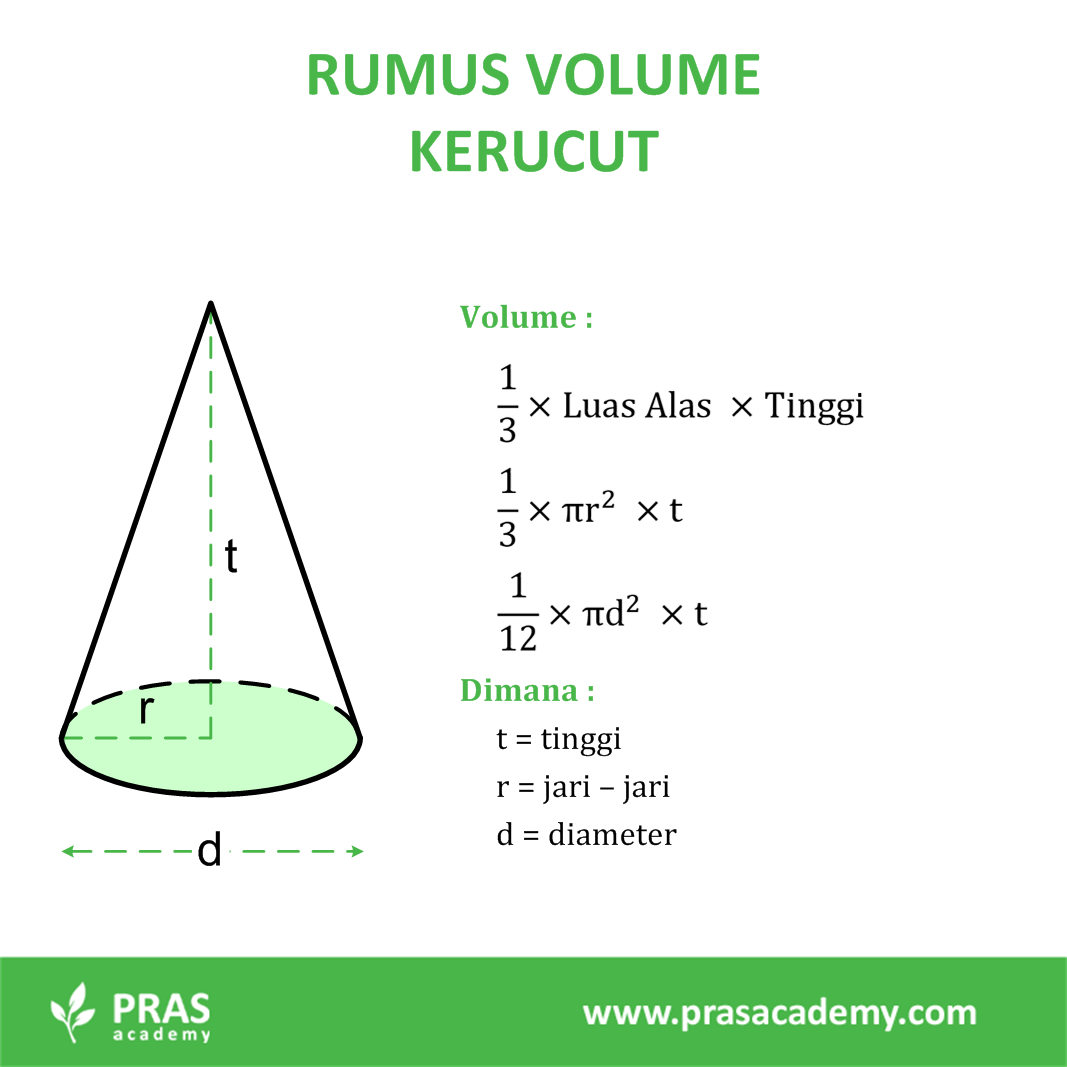
Kerucut adalah bangun ruang tiga dimensi yang memiliki alas berbentuk lingkaran dan sisi tegak yang membentuk satu titik puncak. Rumus volume kerucut:
Volume Kerucut = ⅓ × π × jari-jari2 × tinggi
Contoh: Sebuah kerucut memiliki jari-jari 4 cm dan tinggi 6 cm. Berapakah volumenya? Volume kerucut = ⅓ × π × 4 2 cm 2 × 6 cm ≈ 100,53 cm 3 (menggunakan π ≈ 3,14).
Bola
Bola adalah bangun ruang tiga dimensi yang seluruh titiknya berjarak sama terhadap titik pusat. Rumus volume bola:
Volume Bola = 4⁄ 3 × π × jari-jari 3
Contoh: Sebuah bola memiliki jari-jari 5 cm. Berapakah volumenya? Volume bola = 4⁄ 3 × π × 5 3 cm 3 ≈ 523,6 cm 3 (menggunakan π ≈ 3,14).
Konsep Dasar Volume

Volume dalam matematika menggambarkan ruang yang ditempati oleh suatu benda tiga dimensi. Pemahaman tentang konsep volume sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan sains.
Penjelasan Konsep Dasar Volume
Volume didefinisikan sebagai ukuran ruang yang ditempati oleh suatu benda tiga dimensi. Ukuran ini biasanya dinyatakan dalam satuan kubik, seperti sentimeter kubik (cm³) atau meter kubik (m³). Konsep ini berkaitan erat dengan pengukuran dan perhitungan ruang yang terisi.
Prinsip Pengukuran Volume Bangun Ruang
Pengukuran volume bangun ruang didasarkan pada prinsip mengisi ruang yang ditempati benda tersebut dengan satuan kubus kecil berukuran sama. Jumlah satuan kubus kecil yang dibutuhkan untuk memenuhi ruang tersebut menunjukkan volume bangun ruang tersebut.
- Pengukuran Langsung: Untuk bangun ruang sederhana, volume dapat diukur secara langsung dengan menggunakan alat ukur khusus.
- Pengukuran Tidak Langsung: Untuk bangun ruang yang lebih kompleks, volume dihitung menggunakan rumus matematika yang sesuai dengan bentuk bangun ruang tersebut.
- Satuan Baku: Penggunaan satuan baku seperti cm³, m³, atau liter penting untuk memastikan keseragaman dan akurasi dalam pengukuran.
Faktor-Faktor yang Mempengaruhi Volume Bangun Ruang
Beberapa faktor yang memengaruhi volume bangun ruang adalah:
- Ukuran Panjang, Lebar, dan Tinggi: Pada bangun ruang seperti balok dan kubus, ukuran panjang, lebar, dan tinggi sangat berpengaruh terhadap volumenya.
- Bentuk Bangun Ruang: Bentuk bangun ruang, seperti prisma, limas, tabung, kerucut, dan bola, menentukan rumus yang digunakan untuk menghitung volumenya.
- Material Bangun Ruang: Meskipun material tidak secara langsung mempengaruhi rumus perhitungan volume, material dapat memengaruhi volume yang sebenarnya, jika material tersebut memiliki kepadatan yang berbeda.
Bagan Alir Menghitung Volume Bangun Ruang
Berikut adalah bagan alir umum untuk menghitung volume bangun ruang:
| Langkah | Deskripsi |
|---|---|
| 1. Tentukan Bentuk Bangun Ruang | Identifikasi jenis bangun ruang (balok, kubus, tabung, dll). |
| 2. Identifikasi Dimensi | Cari nilai panjang, lebar, tinggi, jari-jari, dan lain-lain yang diperlukan berdasarkan bentuk bangun ruang. |
| 3. Gunakan Rumus yang Sesuai | Pilih rumus perhitungan volume yang tepat berdasarkan bentuk bangun ruang. |
| 4. Substitusikan Nilai | Masukkan nilai dimensi ke dalam rumus. |
| 5. Hitung Volume | Lakukan perhitungan sesuai rumus. |
| 6. Tuliskan Hasil | Tuliskan hasil perhitungan dengan satuan yang tepat (misalnya, cm³). |
Contoh Soal dan Pembahasan
Berikut ini disajikan beberapa contoh soal menghitung volume bangun ruang, dengan langkah-langkah penyelesaian yang detail. Contoh-contoh soal disusun dengan beragam tingkat kesulitan untuk membantu pemahaman.
Contoh Soal Volume Kubus
Berikut beberapa contoh soal terkait perhitungan volume kubus, beserta langkah-langkah penyelesaiannya.
| Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|
| Sebuah kubus memiliki panjang sisi 5 cm. Berapakah volume kubus tersebut? | Volume kubus dapat dihitung dengan rumus V = s3, di mana s adalah panjang sisi kubus. Dalam soal, panjang sisi (s) = 5 cm. Maka, V = 53 = 5 x 5 x 5 = 125 cm3. |
125 cm3 |
| Jika volume sebuah kubus adalah 27 cm3, berapakah panjang sisi kubus tersebut? | Diketahui volume (V) = 27 cm3. Rumus volume kubus adalah V = s3. Untuk mencari panjang sisi (s), kita perlu mencari akar pangkat tiga dari volume. s = ∛27 = 3 cm. |
3 cm |
Contoh Soal Volume Balok, Materi matematika volume bangun ruang
Berikut contoh soal menghitung volume balok.
| Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|
| Sebuah balok memiliki panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Hitunglah volume balok tersebut! | Volume balok dihitung dengan rumus V = panjang × lebar × tinggi. V = 8 cm × 4 cm × 6 cm = 192 cm3. |
192 cm3 |
| Jika volume sebuah balok adalah 150 cm3, dan panjangnya 5 cm, lebarnya 6 cm, berapakah tingginya? | Diketahui V = 150 cm3, panjang = 5 cm, lebar = 6 cm. V = panjang × lebar × tinggi. 150 = 5 × 6 × tinggi 150 = 30 × tinggi tinggi = 150 / 30 = 5 cm. |
5 cm |
Contoh Soal Volume Limas
Contoh berikut menunjukkan perhitungan volume limas segiempat.
| Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|
| Sebuah limas segiempat beraturan memiliki alas berbentuk persegi dengan panjang sisi 6 cm dan tinggi limas 10 cm. Berapakah volume limas tersebut? | Luas alas persegi = 6 cm × 6 cm = 36 cm2. Volume limas = (1/3) × luas alas × tinggi = (1/3) × 36 cm2 × 10 cm = 120 cm3. |
120 cm3 |
Penerapan dalam Kehidupan Sehari-hari
Pemahaman tentang volume bangun ruang tidak hanya terbatas pada dunia teori. Penerapannya sangat luas dan dapat ditemukan dalam berbagai aktivitas sehari-hari. Mari kita eksplorasi beberapa contoh konkritnya.
Perhitungan Volume dalam Aktivitas Sehari-hari
Kemampuan untuk menghitung volume bangun ruang menjadi penting dalam berbagai situasi praktis. Misalnya, dalam merencanakan kebutuhan material untuk konstruksi atau mengestimasi kapasitas penyimpanan. Berikut beberapa contoh konkret:
- Menghitung Volume Air dalam Bak Mandi: Bayangkan Anda perlu mengetahui berapa banyak air yang dibutuhkan untuk mengisi bak mandi berbentuk prisma. Dengan mengukur panjang, lebar, dan kedalaman bak, Anda dapat menghitung volume air yang dibutuhkan.
- Menghitung Volume Pasir dalam Truk Pengangkut: Truk pengangkut pasir menggunakan bangun ruang prisma untuk mengangkut material. Mengetahui volume prisma yang dibentuk oleh truk sangat penting untuk menentukan berapa banyak pasir yang dapat diangkut. Ini akan membantu dalam efisiensi pengangkutan dan perencanaan proyek.
- Menghitung Volume Semen dalam Beton: Dalam konstruksi, menghitung volume semen yang dibutuhkan untuk campuran beton sangat penting untuk memastikan kualitas dan kekuatan beton yang dihasilkan. Volume bangun ruang berperan dalam perhitungan ini, terutama jika menggunakan cetakan beton dengan bentuk tertentu.
- Desain Wadah Penyimpanan: Dalam industri makanan atau minuman, pemahaman volume bangun ruang penting untuk mendesain wadah penyimpanan yang optimal. Misalnya, desain kaleng minuman atau kemasan makanan. Hal ini berkaitan dengan kapasitas penyimpanan dan efisiensi penggunaan bahan.
Ilustrasi Penerapan
Berikut ilustrasi penerapan perhitungan volume bangun ruang dalam kehidupan sehari-hari. Bayangkan sebuah bak mandi berbentuk balok dengan panjang 1,5 meter, lebar 0,8 meter, dan kedalaman 0,5 meter. Untuk mengisi bak mandi hingga penuh, dibutuhkan volume air sebesar 1,5 m × 0,8 m × 0,5 m = 0,6 m 3. Dengan demikian, Anda perlu menghitung volume balok tersebut untuk mengetahui berapa banyak air yang dibutuhkan.
| Bangun Ruang | Bentuk | Penerapan |
|---|---|---|
| Balok | Kotak persegi panjang | Bak mandi, lemari, kotak penyimpanan |
| Kubus | Kotak dengan sisi sama panjang | Kotak perhiasan, kemasan barang |
| Prisma | Bangun datar yang memiliki dua sisi sejajar dan sama | Truk pengangkut, tangki air |
Ilustrasi lain adalah menghitung volume kerucut untuk menentukan kapasitas wadah kerucut yang digunakan untuk menampung material tertentu. Pengukuran dimensi kerucut akan membantu dalam menghitung volumenya.
Latihan Soal Volume Bangun Ruang: Materi Matematika Volume Bangun Ruang
Berikut ini beberapa latihan soal untuk mengasah pemahaman Anda tentang volume bangun ruang. Setiap soal dilengkapi dengan petunjuk pengerjaan, sehingga Anda dapat menyelesaikannya dengan lebih mudah.
Soal Latihan
Berikut lima soal latihan untuk menguji pemahaman Anda tentang perhitungan volume bangun ruang:
- Kubus: Sebuah kubus memiliki panjang sisi 5 cm. Berapakah volume kubus tersebut?
- Balok: Sebuah balok memiliki panjang 8 cm, lebar 6 cm, dan tinggi 4 cm. Tentukan volume balok tersebut.
- Prisma Segitiga: Sebuah prisma segitiga memiliki alas segitiga dengan alas 6 cm dan tinggi 4 cm. Tinggi prisma adalah 10 cm. Berapakah volume prisma tersebut?
- Limas Segiempat: Sebuah limas segiempat memiliki alas persegi dengan sisi 7 cm dan tinggi limas 12 cm. Berapakah volume limas tersebut?
- Tabung: Sebuah tabung memiliki jari-jari alas 3 cm dan tinggi 10 cm. Berapakah volume tabung tersebut?
Petunjuk Pengerjaan
Berikut panduan untuk menyelesaikan soal-soal latihan:
- Perhatikan bangun ruang yang dijelaskan dalam soal.
- Identifikasi ukuran-ukuran yang diberikan (panjang, lebar, tinggi, jari-jari, dan lain-lain).
- Cari rumus volume yang sesuai dengan bangun ruang tersebut.
- Substitusikan nilai-nilai yang diketahui ke dalam rumus.
- Lakukan perhitungan sesuai dengan urutan operasi hitung.
- Tuliskan hasil akhir dengan satuan yang tepat (cm 3, m 3, dan lain-lain).
Jawaban Soal Latihan
| Soal | Jawaban |
|---|---|
| Kubus dengan sisi 5 cm | 125 cm3 |
| Balok dengan panjang 8 cm, lebar 6 cm, dan tinggi 4 cm | 192 cm3 |
| Prisma Segitiga dengan alas 6 cm, tinggi alas 4 cm, dan tinggi prisma 10 cm | 120 cm3 |
| Limas Segiempat dengan sisi alas 7 cm dan tinggi limas 12 cm | 147 cm3 |
| Tabung dengan jari-jari 3 cm dan tinggi 10 cm | 282.74 cm3 (dibulatkan) |
Ulasan Penutup
Dengan mempelajari materi volume bangun ruang, diharapkan Anda dapat memahami konsep dasar volume dan mengaplikasikannya dalam berbagai situasi. Pemahaman yang baik tentang rumus volume dan penerapannya dalam kehidupan sehari-hari akan sangat membantu dalam memecahkan masalah terkait ukuran dan kapasitas. Semoga materi ini bermanfaat dan memberikan pemahaman yang komprehensif tentang volume bangun ruang.