Materi matematika rotasi kelas 11 akan membahas tentang transformasi geometri yang melibatkan perputaran suatu titik, garis, atau bangun datar di bidang koordinat. Kita akan menjelajahi berbagai aspek rotasi, mulai dari definisi dan jenis-jenisnya, hingga rumus-rumus yang digunakan untuk menentukan koordinat titik setelah rotasi. Dengan pemahaman yang baik tentang materi ini, diharapkan kamu dapat menguasai konsep rotasi dan mengaplikasikannya dalam menyelesaikan soal-soal matematika.
Materi ini akan mencakup penjelasan lengkap tentang definisi rotasi, jenis-jenis rotasi, rumus rotasi, penerapannya dalam soal-soal matematika kelas 11, ilustrasi visual, contoh soal dan pembahasan, serta latihan soal. Melalui pembahasan yang komprehensif, diharapkan kamu dapat memahami dan menguasai materi rotasi dengan baik.
Definisi Rotasi
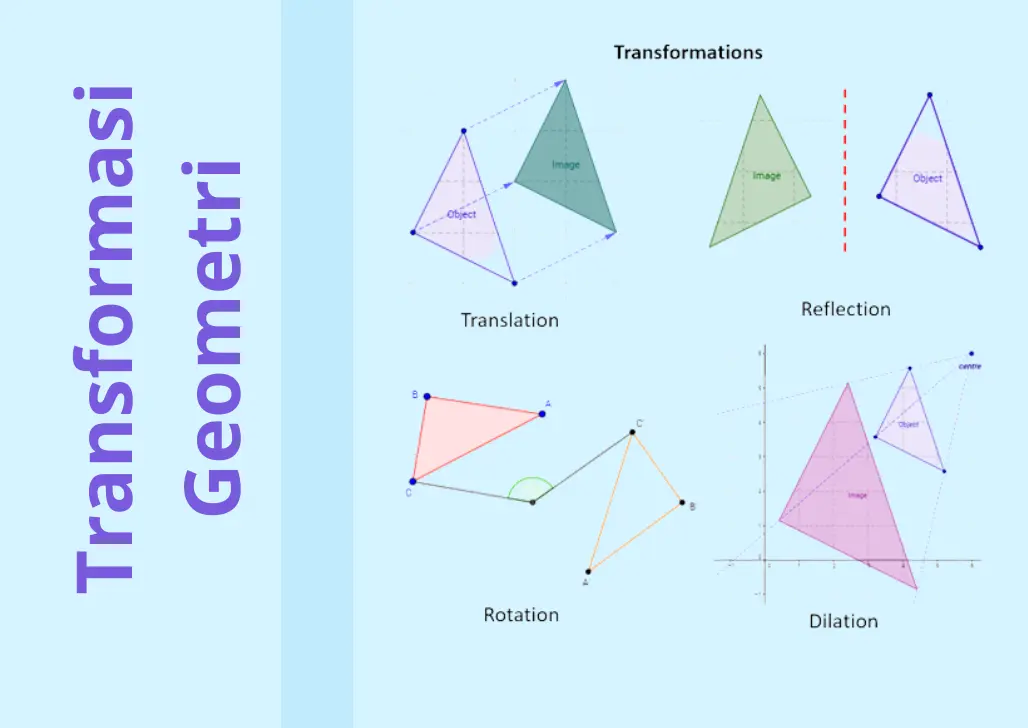
Rotasi merupakan transformasi geometri yang memutar suatu titik atau bangun geometri terhadap suatu titik pusat dengan sudut tertentu. Konsep ini sangat penting dalam memahami geometri dan aplikasinya dalam berbagai bidang, seperti desain grafis, rekayasa, dan pemodelan 3D.
Definisi Matematika Rotasi
Rotasi didefinisikan sebagai transformasi yang memutar suatu titik pada bidang koordinat dengan sudut tertentu terhadap suatu pusat rotasi. Pusat rotasi adalah titik acuan untuk perputaran, sedangkan sudut rotasi adalah besar sudut perputarannya.
Pusat Rotasi dan Sudut Rotasi
Pusat rotasi merupakan titik tetap yang menjadi acuan perputaran. Sudut rotasi menentukan besar perputaran terhadap pusat rotasi tersebut. Sudut positif menunjukkan perputaran berlawanan arah jarum jam, sedangkan sudut negatif menunjukkan perputaran searah jarum jam.
Perbandingan Rotasi dengan Transformasi Geometri Lainnya
| Transformasi | Deskripsi | Contoh |
|---|---|---|
| Rotasi | Memutar suatu objek terhadap titik pusat dengan sudut tertentu. | Memutar jarum jam, memutar roda. |
| Translasi | Menggeser suatu objek sejauh jarak dan arah tertentu. | Menggeser gambar pada layar, memindahkan benda. |
| Refleksi | Memantulkan suatu objek terhadap suatu garis. | Memantulkan bayangan, memantulkan gambar cermin. |
| Dilatasi | Memperbesar atau memperkecil ukuran suatu objek dengan faktor skala tertentu. | Memperbesar atau memperkecil foto, memperbesar atau memperkecil gambar. |
Tabel di atas menunjukkan perbedaan mendasar antara rotasi dengan transformasi geometri lainnya. Masing-masing transformasi memiliki karakteristik dan penerapan yang berbeda-beda.
Jenis-jenis Rotasi
Dalam mempelajari transformasi geometri, rotasi merupakan salah satu jenis transformasi yang penting. Rotasi melibatkan perputaran suatu titik atau bangun geometri terhadap suatu titik pusat dan sudut tertentu. Pemahaman mengenai jenis-jenis rotasi akan mempermudah analisis dan perhitungan dalam berbagai konteks geometri.
Identifikasi Jenis Rotasi Berdasarkan Arah Putaran
Rotasi dapat diidentifikasi berdasarkan arah putarannya, yaitu searah jarum jam atau berlawanan arah jarum jam. Arah putaran ini sangat berpengaruh pada hasil transformasi.
- Rotasi searah jarum jam dilambangkan dengan notasi rotasi yang sesuai.
- Rotasi berlawanan arah jarum jam juga dilambangkan dengan notasi rotasi yang sesuai.
Rotasi pada Bidang Koordinat Kartesius
Pada bidang koordinat kartesius, rotasi didefinisikan sebagai perputaran suatu titik atau bangun geometri terhadap suatu titik pusat yang tetap. Titik pusat rotasi dapat berupa titik asal (0,0) atau titik lain di bidang koordinat.
Memahami koordinat titik awal dan titik pusat rotasi sangat penting untuk menentukan koordinat bayangan setelah rotasi.
Perbedaan Rotasi Berdasarkan Sudut Putaran
Besar sudut putaran juga menentukan jenis rotasi. Rotasi dengan sudut putaran 90°, 180°, dan 270° memiliki karakteristik dan pola transformasi yang berbeda.
| Sudut Putaran | Deskripsi | Pola Transformasi |
|---|---|---|
| 90° | Rotasi dengan sudut 90 derajat, baik searah atau berlawanan arah jarum jam, akan mengubah posisi koordinat titik. | Secara umum, koordinat (x, y) akan berubah menjadi (y, -x) atau (-y, x) tergantung arah putaran. |
| 180° | Rotasi dengan sudut 180 derajat, tidak peduli arah putaran, akan menghasilkan perubahan posisi titik secara simetris terhadap titik pusat. | Koordinat (x, y) akan berubah menjadi (-x, -y). |
| 270° | Rotasi dengan sudut 270 derajat, baik searah atau berlawanan arah jarum jam, memiliki pola transformasi yang serupa dengan rotasi 90 derajat. | Secara umum, koordinat (x, y) akan berubah menjadi (-y, x) atau (y, -x) tergantung arah putaran. |
Dengan memahami perbedaan ini, kita dapat memprediksi posisi bayangan suatu titik atau bangun setelah dirotasikan dengan sudut tertentu.
Rumus Rotasi
Memahami rumus rotasi sangat penting dalam transformasi geometri. Rumus-rumus ini memungkinkan kita menentukan koordinat titik setelah diputar dengan sudut tertentu. Pemahaman ini akan memudahkan kita dalam menganalisis dan menyelesaikan berbagai soal geometri.
Rumus Rotasi Titik terhadap Titik Asal
Berikut adalah rumus rotasi titik (x, y) terhadap titik asal (0, 0) dengan sudut rotasi tertentu.
- Rotasi 90 derajat searah jarum jam: (x’, y’) = (-y, x)
- Rotasi 90 derajat berlawanan arah jarum jam: (x’, y’) = (y, -x)
- Rotasi 180 derajat: (x’, y’) = (-x, -y)
- Rotasi 270 derajat searah jarum jam: (x’, y’) = (y, -x)
- Rotasi 270 derajat berlawanan arah jarum jam: (x’, y’) = (-y, x)
Tabel Rumus Rotasi untuk Sudut Tertentu
Berikut tabel yang merangkum rumus rotasi untuk sudut 90, 180, dan 270 derajat.
| Sudut Rotasi | Rumus Rotasi (berlawanan arah jarum jam) | Rumus Rotasi (searah jarum jam) |
|---|---|---|
| 90° | (x’, y’) = (y, -x) | (x’, y’) = (-y, x) |
| 180° | (x’, y’) = (-x, -y) | (x’, y’) = (-x, -y) |
| 270° | (x’, y’) = (-y, x) | (x’, y’) = (y, -x) |
Contoh Penerapan Rumus Rotasi
Untuk memperjelas pemahaman, berikut contoh penerapan rumus rotasi.
Soal: Titik A(3, 4) dirotasikan 90 derajat berlawanan arah jarum jam terhadap titik asal. Tentukan koordinat titik A’ setelah rotasi.
Rumus rotasi 90 derajat berlawanan arah jarum jam adalah (x’, y’) = (y, -x).
Dengan mengganti nilai x dan y dari titik A(3, 4) ke dalam rumus, kita peroleh:
x’ = 4, y’ = -3
Jadi, koordinat titik A’ setelah rotasi adalah A'(4, -3).
Penerapan Rotasi dalam Materi Matematika Kelas 11
Penerapan rotasi dalam matematika kelas 11 sangat penting untuk memahami transformasi geometri. Pemahaman ini memungkinkan kita menganalisis perubahan posisi titik, garis, dan bangun datar melalui rotasi. Contohnya, dalam fisika, rotasi dapat menjelaskan gerakan benda yang berputar, seperti roda atau planet. Dalam desain grafis, rotasi juga memegang peran krusial dalam mengolah dan memanipulasi objek.
Contoh Penerapan Rotasi dalam Soal Matematika, Materi matematika rotasi kelas 11
Berikut beberapa contoh penerapan rotasi dalam soal-soal matematika kelas 11:
- Rotasi Titik: Menentukan koordinat bayangan suatu titik setelah dirotasikan dengan sudut dan pusat rotasi tertentu.
- Rotasi Garis: Menentukan persamaan garis bayangan setelah dirotasikan. Proses ini melibatkan rotasi setiap titik pada garis tersebut.
- Rotasi Bangun Datar: Menentukan koordinat bayangan titik-titik sudut bangun datar setelah dirotasikan, kemudian menggambar bangun bayangannya.
Penerapan Rotasi dalam Bidang Geometri
Rotasi berperan krusial dalam geometri, khususnya dalam transformasi geometri. Misalnya, rotasi dapat digunakan untuk membuktikan kesebangunan atau kekongruenan bangun datar. Selain itu, rotasi juga dapat digunakan untuk menganalisis simetri suatu bangun datar.
- Simetri Rotasi: Rotasi digunakan untuk menentukan sudut rotasi terkecil yang dapat memutar suatu bangun datar sehingga menempati bingkainya kembali.
- Transformasi Geometri: Rotasi adalah salah satu transformasi geometri yang mengubah posisi suatu bangun datar di bidang koordinat.
- Pembuktian Kesebangunan/Kekongruenan: Dengan menerapkan rotasi, kita dapat memindahkan bangun datar dan membandingkan sisi-sisi atau sudut-sudutnya untuk menentukan kesebangunan atau kekongruenan.
Penerapan Rotasi dalam Bidang Trigonometri
Penerapan rotasi dalam trigonometri umumnya terkait dengan analisis sudut dan perbandingan trigonometri. Misalnya, pergeseran sudut dapat diinterpretasikan sebagai rotasi pada lingkaran satuan.
- Analisis Sudut: Rotasi dapat digunakan untuk menganalisis hubungan antara sudut-sudut yang berbeda dalam suatu segitiga atau bangun datar.
- Perbandingan Trigonometri: Dalam konteks lingkaran satuan, rotasi titik pada lingkaran tersebut dapat dikaitkan dengan perbandingan trigonometri dari sudut yang dibentuk oleh titik tersebut dengan sumbu x.
- Penerapan dalam Kalkulus: Penerapan rotasi juga terlihat dalam kalkulus, misalnya pada perhitungan volume benda putar.
Contoh Soal Rotasi Titik
Tentukan koordinat bayangan titik A(2, 3) setelah dirotasikan 90 derajat searah jarum jam dengan pusat O(0, 0).
Jawaban: Koordinat bayangan titik A adalah (-3, 2).
Contoh Soal Rotasi Garis
Tentukan persamaan garis bayangan dari garis y = 2x + 1 setelah dirotasikan 90 derajat berlawanan arah jarum jam dengan pusat O(0, 0).
Jawaban: Persamaan garis bayangan adalah x = -1/2y + 1/2.
Ilustrasi Rotasi
Memahami rotasi lebih mudah dengan melihat contoh visual. Berikut ilustrasi rotasi titik dan bangun datar pada bidang koordinat.
Ilustrasi Rotasi Titik
Bayangkan sebuah titik A(2, 3) di bidang koordinat. Untuk memutar titik A sebesar 90 derajat berlawanan arah jarum jam terhadap titik pusat (0, 0), kita perlu menerapkan aturan rotasi. Hasil rotasinya akan menjadi titik A’ dengan koordinat baru. Perhatikan perubahan koordinat x dan y yang terjadi.
Ilustrasi Rotasi Bangun Datar
Selain titik, rotasi juga dapat diterapkan pada bangun datar seperti segitiga dan persegi. Ilustrasi berikut memperlihatkan rotasi segitiga ABC sebesar 180 derajat berlawanan arah jarum jam terhadap titik pusat (1, 1). Perhatikan bagaimana setiap titik sudut segitiga berputar dan membentuk segitiga A’B’C’.
Langkah-Langkah Menggambar Rotasi
- Tentukan titik pusat rotasi dan sudut rotasi.
- Tentukan koordinat titik-titik pada bangun datar yang akan dirotasikan.
- Terapkan aturan rotasi yang sesuai untuk setiap titik. Jika rotasinya berlawanan arah jarum jam, koordinat x dan y perlu diubah sesuai rumus rotasi. Jika searah jarum jam, aturannya berbeda.
- Plot titik-titik hasil rotasi pada bidang koordinat untuk membentuk bangun datar yang baru.
- Hubungkan titik-titik hasil rotasi untuk membentuk bangun datar yang dirotasikan.
Dengan mengikuti langkah-langkah ini, Anda dapat menggambar rotasi pada berbagai bangun datar dengan mudah. Penting untuk memahami aturan rotasi dan koordinat titik-titik pada bangun datar.
Contoh Rotasi Persegi
Misalnya, sebuah persegi dengan titik sudut A(1, 1), B(4, 1), C(4, 4), dan D(1, 4) dirotasikan sebesar 90 derajat berlawanan arah jarum jam terhadap titik pusat (2, 2). Dengan menerapkan aturan rotasi, titik A'(1, 1) akan berubah menjadi A'(1, 1)’. Begitu seterusnya untuk titik-titik lainnya. Setelah dirotasikan, akan terbentuk persegi baru dengan titik-titik sudut yang berbeda.
Contoh Soal dan Pembahasan Rotasi

Berikut ini disajikan beberapa contoh soal rotasi beserta pembahasannya. Contoh-contoh ini dirancang untuk memberikan pemahaman yang lebih mendalam tentang penerapan konsep rotasi dalam koordinat kartesius.
Contoh Soal 1: Rotasi Titik pada Koordinat
Tentukan bayangan titik A(2, 3) setelah dirotasikan sebesar 90 derajat berlawanan arah jarum jam terhadap titik pusat O(0, 0).
- Identifikasi Data: Titik A(2, 3), sudut rotasi 90 derajat berlawanan arah jarum jam, dan titik pusat rotasi O(0, 0).
- Penerapan Rumus Rotasi: Rumus rotasi titik (x, y) sebesar θ derajat terhadap titik pusat (a, b) adalah:
- Substitusi Nilai: Dalam kasus ini, a = 0, b = 0, θ = 90 derajat, x = 2, dan y = 3.
- Perhitungan:
- cos 90° = 0
- sin 90° = 1
Substitusikan nilai-nilai tersebut ke dalam rumus:
- x’ = (2 – 0)
– 0 – (3 – 0)
– 1 + 0 = -3 - y’ = (2 – 0)
– 1 + (3 – 0)
– 0 + 0 = 2
- Kesimpulan: Bayangan titik A setelah dirotasikan adalah A'( -3, 2).
x’ = (x – a) cos θ
(y – b) sin θ + a
y’ = (x – a) sin θ + (y – b) cos θ + b
Contoh Soal 2: Rotasi Bangun Datar
Sebuah segitiga dengan titik sudut A(1, 2), B(4, 5), dan C(3, 1) dirotasikan 180 derajat terhadap titik pusat (2, 3). Tentukan koordinat bayangan ketiga titik tersebut.
- Identifikasi Data: Titik A(1, 2), B(4, 5), C(3, 1), sudut rotasi 180 derajat, dan titik pusat rotasi (2, 3).
- Penerapan Rumus Rotasi: Gunakan rumus rotasi yang sama seperti pada contoh soal sebelumnya, dengan θ = 180 derajat, a = 2, dan b = 3.
- Perhitungan (untuk titik A):
- cos 180° = -1
- sin 180° = 0
Substitusikan nilai-nilai tersebut ke dalam rumus untuk mendapatkan koordinat A’:
- x’ = (1 – 2)
– -1 – (2 – 3)
– 0 + 2 = 1 - y’ = (1 – 2)
– 0 + (2 – 3)
– -1 + 3 = 2
Lakukan perhitungan serupa untuk titik B dan C.
- Kesimpulan: Bayangan titik A adalah A'(1, 2), B’ dan C’ adalah … (Hasil perhitungan untuk B dan C).
Contoh Soal 3: Rotasi pada Bidang Koordinat yang Kompleks
Sebuah persegi panjang dengan titik sudut A(0, 0), B(4, 0), C(4, 2), dan D(0, 2) dirotasikan 270 derajat searah jarum jam terhadap titik pusat (1, 1). Tentukan koordinat bayangan keempat titik tersebut.
- Identifikasi Data: Titik A(0, 0), B(4, 0), C(4, 2), D(0, 2), sudut rotasi 270 derajat searah jarum jam, dan titik pusat rotasi (1, 1).
- Penerapan Rumus Rotasi: Gunakan rumus rotasi yang sama seperti pada contoh soal sebelumnya, dengan θ = 270 derajat, a = 1, dan b = 1.
- Perhitungan (untuk titik A): Lakukan perhitungan serupa seperti contoh soal sebelumnya. Perhatikan arah rotasi.
- Kesimpulan: Bayangan titik A adalah A'(…), B’ adalah (…), C’ adalah (…), dan D’ adalah (…). (Hasil perhitungan untuk semua titik).
Latihan Soal Rotasi: Materi Matematika Rotasi Kelas 11
Berikut ini adalah latihan soal rotasi untuk mengasah pemahaman Anda tentang materi ini. Setiap soal dirancang untuk menguji pemahaman Anda dalam menerapkan konsep rotasi pada bidang koordinat.
Soal Latihan Rotasi
Berikut ini 5 soal latihan rotasi yang dapat Anda selesaikan:
- Tentukan bayangan titik A(2, 3) setelah dirotasikan sebesar 90 derajat berlawanan arah jarum jam terhadap titik pusat (0, 0).
- Sebuah titik B(–4, 1) dirotasikan sebesar 180 derajat terhadap titik pusat (0, 0). Tentukan koordinat bayangan titik B setelah rotasi.
- Tentukan bayangan titik C(5, -2) setelah dirotasikan sebesar 270 derajat searah jarum jam terhadap titik pusat (0, 0). Gambarkan titik C dan bayangannya pada bidang koordinat.
- Tentukan bayangan titik D(–1, 6) setelah dirotasikan sebesar 90 derajat searah jarum jam terhadap titik pusat (1, 2).
- Sebuah segitiga ABC dengan titik sudut A(1, 2), B(4, 5), dan C(3, 1) dirotasikan sebesar 180 derajat berlawanan arah jarum jam terhadap titik pusat (2, 3). Tentukan koordinat bayangan ketiga titik sudut segitiga tersebut.
Petunjuk dan Tips
Berikut beberapa petunjuk dan tips untuk menyelesaikan soal-soal tersebut:
- Pahami konsep rotasi pada bidang koordinat. Ingatlah bahwa rotasi mengubah posisi suatu titik dengan memutarnya terhadap suatu titik pusat dengan sudut tertentu.
- Gambarlah titik-titik dan pusat rotasi pada bidang koordinat untuk mempermudah visualisasi.
- Perhatikan arah rotasi (berlawanan atau searah jarum jam).
- Jika titik pusat rotasi bukan (0, 0), perlu dihitung terlebih dahulu pergeseran titik ke pusat koordinat dan kemudian dirotasikan. Setelah dirotasikan, titik tersebut digeser kembali sesuai dengan titik pusat rotasi.
- Untuk soal yang melibatkan segitiga, rotasikan masing-masing titik sudut segitiga tersebut.
Kunci Jawaban
Berikut kunci jawaban untuk setiap soal latihan:
| No Soal | Kunci Jawaban |
|---|---|
| 1 | A'(–3, 2) |
| 2 | B'(4, –1) |
| 3 | C'(2, 5) |
| 4 | D'(–3, 4) |
| 5 | A'(3, 4), B'(2, 1), C'(1, 5) |
Simpulan Akhir
Semoga materi rotasi ini dapat memberikan pemahaman yang mendalam dan membantu kamu dalam menyelesaikan soal-soal matematika kelas 11. Dengan menguasai konsep rotasi, kamu akan lebih siap menghadapi berbagai permasalahan geometri dan trigonometri yang mungkin muncul. Jangan ragu untuk berlatih dan bertanya jika ada yang kurang jelas. Selamat belajar!