Materi matematika lebih besar lebih kecil merupakan fondasi penting dalam pemahaman perbandingan bilangan. Topik ini akan membahas berbagai jenis bilangan, mulai dari bilangan bulat, pecahan, hingga desimal, serta bagaimana membandingkannya menggunakan simbol “lebih besar dari” dan “lebih kecil dari”.
Dengan memahami konsep dasar perbandingan ini, kita akan mampu menyelesaikan berbagai soal cerita dan aplikasi matematika lainnya. Materi ini akan dijelaskan dengan contoh-contoh konkret, ilustrasi visual, dan latihan soal untuk mempermudah pemahaman.
Definisi dan Konsep Dasar Perbandingan
Memahami perbandingan lebih besar dan lebih kecil merupakan dasar penting dalam matematika. Dengan pemahaman yang kuat, kita dapat membandingkan nilai-nilai dan mengurutkannya dengan tepat.
Definisi Perbandingan Lebih Besar dan Lebih Kecil
Perbandingan lebih besar dan lebih kecil digunakan untuk membandingkan dua nilai. Nilai yang lebih besar memiliki besaran yang lebih tinggi dibandingkan nilai yang lebih kecil. Konsep ini sangat penting dalam berbagai bidang, seperti dalam mengurutkan angka, menyelesaikan pertidaksamaan, dan berbagai aplikasi lainnya.
Notasi dan Simbol Perbandingan
Untuk menyatakan perbandingan lebih besar atau lebih kecil, kita menggunakan simbol-simbol khusus. Perhatikan perbedaan notasi berikut:
- Lebih besar dari (>): Simbol ini digunakan untuk menunjukkan bahwa nilai di sebelah kiri lebih besar dari nilai di sebelah kanan.
- Lebih kecil dari (<): Simbol ini digunakan untuk menunjukkan bahwa nilai di sebelah kiri lebih kecil dari nilai di sebelah kanan.
Contoh Konkret
Berikut beberapa contoh konkret untuk memperjelas perbedaan konsep:
- 5 > 2 (Lima lebih besar dari dua)
- 10 < 15 (Sepuluh lebih kecil dari lima belas)
- −3 < 0 (Minus tiga lebih kecil dari nol)
- 8 > −1 (Delapan lebih besar dari minus satu)
Tabel Simbol Perbandingan
| Simbol | Notasi | Contoh |
|---|---|---|
| > | Lebih besar dari | 10 > 5 |
| < | Lebih kecil dari | 2 < 7 |
Ilustrasi Visual
Ilustrasi garis bilangan dapat digunakan untuk memperjelas konsep “lebih besar” dan “lebih kecil”. Pada garis bilangan, angka yang lebih besar terletak di sebelah kanan angka yang lebih kecil. Misalnya, angka 5 terletak di sebelah kanan angka 2, sehingga 5 lebih besar dari 2.
Bayangkan garis bilangan yang memanjang dari kiri ke kanan. Angka-angka pada garis bilangan disusun secara berurutan, dengan angka-angka yang lebih besar terletak di sebelah kanan angka yang lebih kecil.
Perbandingan Bilangan Bulat
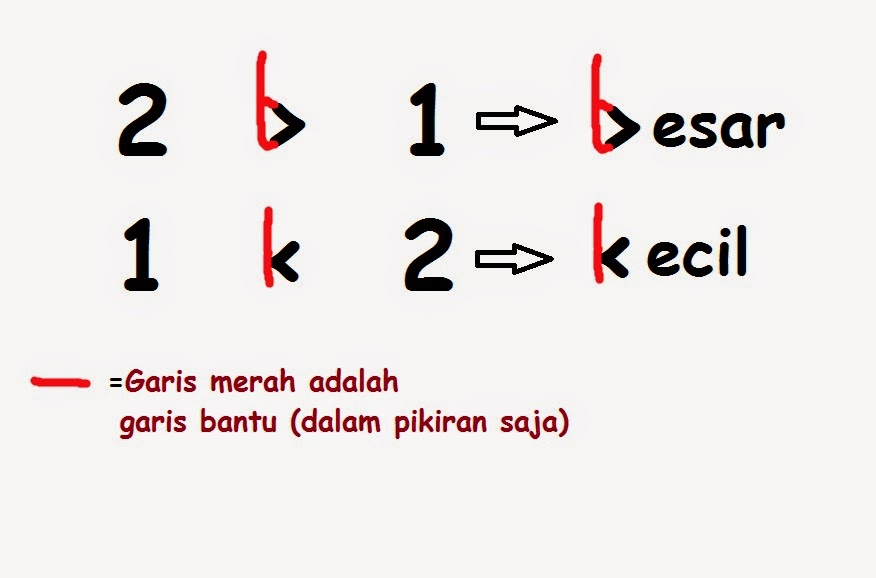
Memahami perbandingan bilangan bulat sangat penting dalam matematika. Kemampuan membandingkan bilangan bulat memungkinkan kita menyelesaikan berbagai masalah dalam kehidupan sehari-hari, seperti mengurutkan nilai atau membandingkan keuntungan dan kerugian.
Contoh Bilangan Bulat Positif dan Negatif
Bilangan bulat terdiri dari bilangan bulat positif, bilangan nol, dan bilangan bulat negatif. Berikut beberapa contoh:
- Bilangan bulat positif: 1, 2, 3, 4, 5, 10, 100
- Bilangan bulat negatif: -1, -2, -3, -4, -5, -10, -100
Perbandingan Bilangan Bulat dengan Simbol
Kita dapat membandingkan bilangan bulat dengan menggunakan simbol “lebih besar dari” (>) dan “lebih kecil dari” ( <). Contohnya:
- 5 > 2 (5 lebih besar dari 2)
- -3 < 1 (-3 lebih kecil dari 1)
- -10 < -5 (-10 lebih kecil dari -5)
Tabel Perbandingan Bilangan Bulat
Tabel berikut menunjukkan contoh perbandingan bilangan bulat beserta alasannya:
| Bilangan Pertama | Simbol | Bilangan Kedua | Alasan |
|---|---|---|---|
| 5 | > | -2 | Bilangan positif selalu lebih besar dari bilangan negatif |
| -8 | < | -3 | Bilangan negatif yang nilainya lebih kecil bernilai lebih besar |
| 0 | > | -10 | Bilangan nol selalu lebih besar dari bilangan negatif |
Perbandingan Bilangan Bulat pada Garis Bilangan
Garis bilangan dapat digunakan untuk membandingkan bilangan bulat. Bilangan yang lebih besar terletak di sebelah kanan pada garis bilangan.
Misalnya, -2 berada di sebelah kiri 3 pada garis bilangan, sehingga -2 lebih kecil dari 3.
Aturan Dasar dalam Membandingkan Bilangan Bulat
- Bilangan bulat positif selalu lebih besar dari bilangan bulat negatif.
- Bilangan nol lebih besar dari bilangan bulat negatif.
- Pada bilangan bulat negatif, semakin kecil nilainya, semakin besar nilainya.
- Untuk membandingkan bilangan negatif, kita perhatikan nilai absolutnya. Bilangan negatif dengan nilai absolut lebih kecil lebih besar nilainya.
Perbandingan Bilangan Pecahan: Materi Matematika Lebih Besar Lebih Kecil

Membandingkan bilangan pecahan adalah keterampilan penting dalam matematika. Memahami cara membandingkan pecahan memungkinkan kita untuk menentukan mana yang lebih besar atau lebih kecil, dan ini sangat berguna dalam berbagai situasi, mulai dari menghitung bahan dalam resep hingga membandingkan harga barang.
Contoh Bilangan Pecahan
Berikut beberapa contoh bilangan pecahan:
- 1/2
- 3/4
- 2/5
- 5/8
- 7/10
Perbandingan Bilangan Pecahan, Materi matematika lebih besar lebih kecil
Untuk membandingkan bilangan pecahan, kita perlu menentukan mana yang lebih besar atau lebih kecil. Kita dapat menggunakan simbol “lebih besar dari” (>) dan “lebih kecil dari” ( <).
Metode Perbandingan Pecahan
Beberapa metode yang dapat digunakan untuk membandingkan pecahan meliputi:
- Menyamakan penyebut: Metode ini melibatkan mengubah pecahan-pecahan menjadi pecahan senilai dengan penyebut yang sama. Kemudian, kita dapat membandingkan pembilangnya. Pecahan dengan pembilang lebih besar adalah pecahan yang lebih besar.
- Menggunakan garis bilangan: Memvisualisasikan pecahan pada garis bilangan dapat membantu kita membandingkannya. Pecahan yang lebih ke kanan pada garis bilangan adalah pecahan yang lebih besar.
- Menggunakan perbandingan silang: Metode ini melibatkan perkalian silang pembilang dan penyebut pecahan-pecahan. Pecahan dengan hasil perkalian silang yang lebih besar adalah pecahan yang lebih besar.
Tabel Perbandingan Pecahan
| Pecahan | Hasil Perbandingan | Langkah Perbandingan |
|---|---|---|
| 1/2 dan 3/4 | 1/2 < 3/4 | Menyamakan penyebut: 1/2 = 2/4. 2/4 < 3/4 |
| 2/5 dan 5/8 | 2/5 < 5/8 | Menyamakan penyebut: 2/5 = 16/40, 5/8 = 25/40. 16/40 < 25/40 |
| 7/10 dan 3/5 | 7/10 > 3/5 | Menyamakan penyebut: 7/10 = 7/10, 3/5 = 6/10. 7/10 > 6/10 |
Penerapan dalam Kehidupan Sehari-hari
Perbandingan pecahan sering digunakan dalam berbagai konteks kehidupan sehari-hari. Misalnya, ketika kita membeli bahan makanan, kita mungkin perlu membandingkan harga per satuan untuk menentukan mana yang lebih ekonomis. Contoh lain adalah saat kita mengukur bahan dalam resep, di mana perbandingan pecahan digunakan untuk memastikan proporsi yang tepat.
Perbandingan Bilangan Desimal
Memahami cara membandingkan bilangan desimal sangat penting dalam matematika. Kemampuan ini berguna dalam berbagai situasi, seperti membandingkan harga barang, mengukur panjang, atau menyelesaikan perhitungan lainnya.
Contoh Bilangan Desimal
Berikut beberapa contoh bilangan desimal:
- 3,14
- 0,5
- 2,75
- 10,01
- 0,002
Membandingkan Bilangan Desimal
Untuk membandingkan bilangan desimal, kita perlu memperhatikan nilai tempat masing-masing digit. Perhatikan angka pada bagian bilangan bulat, kemudian pada bagian desimal. Langkah-langkahnya dijelaskan pada tabel berikut:
| Langkah | Penjelasan | Contoh |
|---|---|---|
| 1. Bandingkan bilangan bulat | Jika bilangan bulat berbeda, bilangan dengan bilangan bulat lebih besar akan lebih besar. | Membandingkan 2,5 dan 12,3. Bilangan bulat 2 dan 12, maka 12 lebih besar dari 2. |
| 2. Bandingkan angka di bagian desimal | Jika bilangan bulat sama, bandingkan angka di bagian desimal dari kiri ke kanan. | Membandingkan 5,2 dan 5,25. Bagian bilangan bulat sama (5), maka bandingkan bagian desimal (2 dan 25). |
| 3. Tentukan simbol perbandingan | Gunakan simbol “lebih besar dari” (>) atau “lebih kecil dari” (<) untuk menunjukkan hasil perbandingan. | 5,2 < 5,25. |
Ilustrasi pada Garis Bilangan
Menggambarkan bilangan desimal pada garis bilangan dapat membantu memahami posisi dan perbandingannya. Misalnya, untuk membandingkan 2,5 dan 3,1, kita bisa menempatkan kedua bilangan tersebut pada garis bilangan. Bilangan 3,1 akan berada di sebelah kanan 2,5, menunjukkan bahwa 3,1 lebih besar dari 2,5.
Aturan Perbandingan Bilangan Desimal
- Perhatikan bilangan bulat terlebih dahulu. Bilangan dengan bilangan bulat lebih besar akan lebih besar.
- Jika bilangan bulat sama, bandingkan digit desimal mulai dari digit pertama di sebelah kanan tanda koma. Digit yang lebih besar menunjukkan bilangan yang lebih besar.
- Jika semua digit desimal sama, maka kedua bilangan desimal tersebut sama nilainya.
Penerapan dalam Konteks Matematika
Memahami konsep “lebih besar” dan “lebih kecil” sangat penting dalam berbagai penerapan matematika. Konsep ini membentuk dasar untuk membandingkan nilai-nilai dan menyelesaikan masalah yang melibatkan perbandingan.
Contoh Soal Cerita
Berikut beberapa contoh soal cerita yang melibatkan perbandingan “lebih besar” dan “lebih kecil”:
- Ani memiliki 15 buah apel, sedangkan Budi memiliki 10 buah apel. Siapa yang memiliki apel lebih banyak?
- Sebuah toko menjual baju seharga Rp50.000, sedangkan baju yang sama di toko lain seharga Rp45.000. Di mana harga baju lebih murah?
- Berat sebuah karung beras adalah 50 kg, sedangkan berat karung beras lainnya 45 kg. Manakah yang lebih berat?
Langkah-Langkah Pemecahan Masalah
Untuk menyelesaikan soal cerita yang melibatkan perbandingan “lebih besar” dan “lebih kecil”, ikuti langkah-langkah berikut:
- Baca dan pahami soal cerita dengan cermat.
- Identifikasi nilai-nilai yang diberikan dalam soal.
- Tentukan apa yang ditanyakan dalam soal.
- Bandingkan nilai-nilai yang diberikan untuk menentukan mana yang lebih besar atau lebih kecil.
- Tuliskan jawaban yang sesuai dengan pertanyaan dalam soal.
Contoh Soal dan Penyelesaian
| Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|
| Sebuah toko menjual buku tulis seharga Rp5.000 dan pensil seharga Rp2.000. Manakah yang lebih mahal? | Langkah 1: Identifikasi nilai harga buku tulis (Rp5.000) dan pensil (Rp2.000). Langkah 2: Bandingkan kedua nilai. Rp5.000 lebih besar dari Rp2.
000. Langkah 3 Tuliskan jawaban. Buku tulis lebih mahal. |
Buku tulis |
| Berat sebuah kotak mainan adalah 2 kg dan berat sebuah boneka adalah 1 kg. Manakah yang lebih ringan? | Langkah 1: Identifikasi nilai berat kotak mainan (2 kg) dan boneka (1 kg). Langkah 2: Bandingkan kedua nilai. 1 kg lebih kecil dari 2 kg. Langkah 3: Tuliskan jawaban. Boneka lebih ringan. | Boneka |
| Suhu di Jakarta adalah 30°C dan suhu di Bandung adalah 25°C. Manakah yang lebih panas? | Langkah 1: Identifikasi nilai suhu Jakarta (30°C) dan Bandung (25°C). Langkah 2: Bandingkan kedua nilai. 30°C lebih besar dari 25°C. Langkah 3: Tuliskan jawaban. Suhu di Jakarta lebih panas. | Suhu di Jakarta |
Penerapan dalam Matematika Lainnya
Konsep perbandingan “lebih besar” dan “lebih kecil” merupakan dasar dalam berbagai materi matematika lainnya, seperti:
- Operasi hitung: Penjumlahan, pengurangan, perkalian, dan pembagian melibatkan perbandingan nilai.
- Pecahan: Perbandingan antara bagian dan keseluruhan.
- Persen: Perbandingan suatu nilai dengan 100.
- Statistika: Perbandingan data untuk mengidentifikasi tren dan pola.
Latihan dan Soal
Untuk mengasah pemahaman tentang perbandingan, berikut beberapa latihan soal dengan berbagai tingkatan kesulitan. Soal-soal ini dirancang untuk membantu Anda mempraktikkan penerapan konsep perbandingan dalam berbagai situasi.
Contoh Soal Pilihan Ganda
Berikut beberapa contoh soal pilihan ganda yang berkaitan dengan perbandingan:
- Jika perbandingan umur Ani dan Budi adalah 2 : 3, dan umur Ani 10 tahun, maka umur Budi adalah:
- a. 12 tahun
- b. 15 tahun
- c. 18 tahun
- d. 20 tahun
- Perbandingan jumlah buku matematika dan bahasa Indonesia di perpustakaan adalah 3 :
Jika jumlah buku matematika 12 buah, maka jumlah buku bahasa Indonesia adalah:
- a. 15
- b. 20
- c. 25
- d. 30
Contoh Soal Uraian
Berikut beberapa contoh soal uraian yang mengharuskan penjelasan alasan perbandingan:
- Harga sebuah apel adalah Rp5.000, dan harga sebuah jeruk adalah Rp3.000. Tentukan perbandingan harga apel dan jeruk. Jelaskan alasan perbandingannya.
- Sebuah toko menjual dua jenis pensil dengan harga yang berbeda. Pensil jenis A seharga Rp2.000 dan pensil jenis B seharga Rp3.000. Jika seseorang membeli 4 pensil jenis A dan 6 pensil jenis B, tentukan perbandingan total harga pensil jenis A dan B. Jelaskan langkah-langkah dan alasan perhitungan Anda.
Tabel Soal Latihan, Kunci Jawaban, dan Langkah Penyelesaian
| No | Soal | Kunci Jawaban | Langkah Penyelesaian |
|---|---|---|---|
| 1 | Perbandingan tinggi badan Rika dan Dinda adalah 5 : 6. Jika tinggi badan Rika 120 cm, berapa tinggi badan Dinda? | 144 cm | 5/6 = 120/x x = (6/5) – 120 = 144 cm |
| 2 | Sebuah toko kue menjual kue coklat dan kue keju dengan perbandingan 2 : 3. Jika dalam sehari terjual 15 kue keju, berapa banyak kue coklat yang terjual? | 10 kue | 2/3 = x/15, x = (2/3) – 15 = 10 kue |
| 3 | Umur Ayah : Ibu = 4 : 3. Jika umur Ayah 32 tahun, berapakah umur Ibu? | 24 tahun | 4/3 = 32/x, x = (3/4) – 32 = 24 tahun |
Ringkasan Penutup
Dengan mempelajari materi matematika lebih besar lebih kecil, kita telah mengasah kemampuan dalam membandingkan berbagai jenis bilangan. Semoga pemahaman ini dapat diterapkan dalam berbagai situasi dan membantu dalam menyelesaikan permasalahan matematika di masa mendatang. Materi ini membuka pintu untuk menjelajahi konsep matematika yang lebih kompleks.